Phase Transformations and Growth of Biological Tissue
Grain (Growth and Grain Refinement)
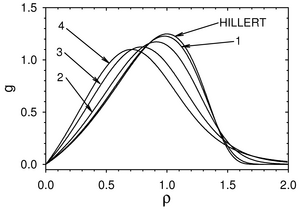
The classical concept of Lifshitz-Slyozov-Wagner is extended to a finite volume fraction of precipitates. A dimension-free distribution function is introduced depending on a dimension-free radius (R/Rc with Rc as critical grain radius) and on time offering a stationarity indicator for any initial grain size distribution. The topic of grain refinement is also dealt with this concept.
Finite Element Modeling of the Cyclic Wetting Mechanism in Wheat Awns
Finite Element Modeling of the Cyclic Wetting Mechanism in Wheat Awns
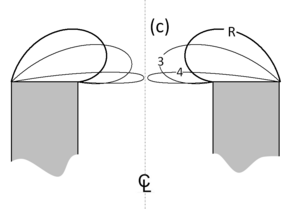
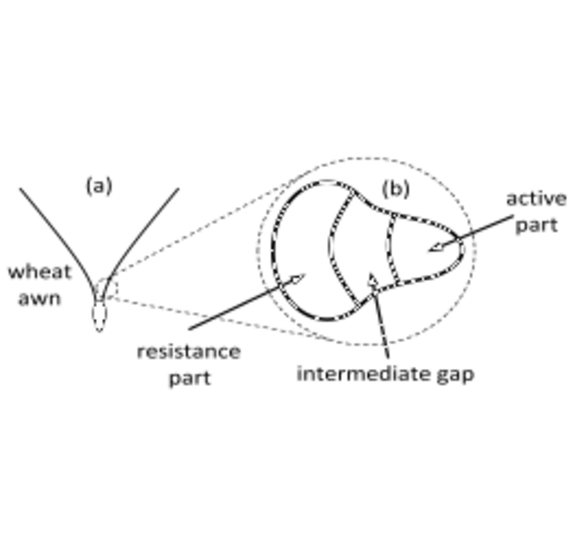
Awns and appendages on the seed dispersal unit play an important role in dispersing the seed to the germination site. The seed unit of the wild wheat plants (Triticum turgidum ssp. dicoccoides) is assembled of two pronounced awns that stabilize the dispersal fall off from the mother plant. Although consisting only of dead tissue, wheat awns work like muscles, being able to propel seeds several millimeters into the soil. The cross-section of the awn consists macroscopically of an active part, an intermediate gap and a resistance part, all of them consisting of hollow cylindrical cells. The active part is responsible for the awn bending with changing ambient humidity. It is built of cylindrical cells containing layers with parallel cellulose fibrils embedded in a soft hygroscopic matrix. It was shown that the active and resistance part expand differently at varying humidity, pushing the awns together with increasing moisture and pulling them apart while drying. In the present study, a single cylindrical cell of the active part is modeled as plywood architecture with the finite elements, especially focusing on the specific microscopic features. Based on earlier experimental findings the cell wall is modeled as a multilayered cylindrical tube with alternating cellulose fiber orientation in successive layers. It is shown that swelling upon hydration leads to the formation of gaps between neighboring layers, which could act as nanometer-sized valves, thus enabling the entry of humidity into the cell wall. This finding supports the hypothesis that the plywood-like arrangement of cellulose fibrils enhances the effect of ambient humidity by accelerating water or vapor diffusion along gaps. The model shows that a certain distribution of fibers with tangential and axial orientation is necessary to enable an opening of the gaps between cell wall layers.
Tissue Growth
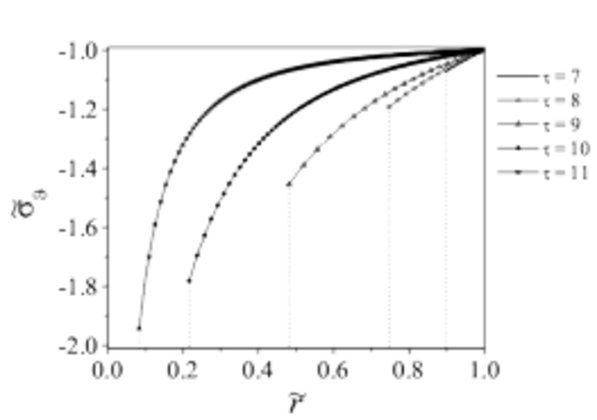
Research in this field is focussed on thermodynamically consistent modelling of tissue growth in living materials such as bone, and the activities are carried out in cooperation with the department of Biomaterials of Max-Planck-Institute in Golm (Director: Prof. P. Fratzl) within the research group of Dr. Dunlop. It is a goal to derive evolution equations so that the experimentally observed coupling between the growth of new material and the local deformation or stress state can be mapped in an according way. Theory has been applied to model tissue growth in a simple geometrical setting, namely tissue growth confined inside a circular hole [1]. The results of the calculations can be compared with experimental findings [2]. However, in case of growth on convex surfaces the predicted exponential growth behaviour is in contrast to experimental results where no growth, apart from the formation of a thin monolayer of cells, is observed. There is experimental evidence that actin fibers can act as “contractile” elements. This is considered in a more advanced model by introducing a surface stress term [3] so that both inward and outward growth can be modelled in a realistic way.
[1] W.C. Dunlop, F. D. Fischer, E. Gamsjäger and P. Fratzl, Journal of the Mechanics and Physics of Solids (2010) 58(8), 1073-1087.[2] M. Rumpler, A. Woesz, J. W. C. Dunlop, J. T. van Dongen, P. Fratzl, (2008), Journal of the Royal Society Interface 5(27): 1173-1180.[3] E. Gamsjäger, J. W.C. Dunlop, F. D. Fischer, C. Bidan and P. Fratzl: "The role of surface stress on the kinetics of tissue growth in confined geometries", (in preparation for Acta Biomaterialia).